The Traffic Accident Reconstruction Origin -Approach Angles Solution-

The questions posed are:

1) Why do we pull Drag Sleds through their center of mass?

Answer: There is no good reason to require that a drag sled be pulled through its center of mass. In fact, there is a good reason for not doing so.

A bit of background is in order.

We divide motion up into two types -

1. Translational motion. This is movement of the center of mass, treating the object like a particle with all its mass located at that point. An example of translational motion is a bullet traveling from a gun to the target.
2. Rotational motion. Rotation is usually measured about an object's center of mass. An example of rotational motion would be the spin on a bullet as it translates to the target.

Newton's Laws apply to translation and rotation separately. The translational laws are the well known ones linking force, mass and acceleration. The rotation laws have the same form but force is replaced by torque, mass by moment of inertia and translational acceleration in metres/s² (ft/s²) by rotational acceleration in radians/s².

Translational acceleration is proportional to the resultant force applied to the mass. This is Newton's Second law (F = ma). A resultant is the sum of all the forces applied to an object. In the case of the drag sled we must consider forces in two directions, the X (horizontal) and Y (vertical) directions.

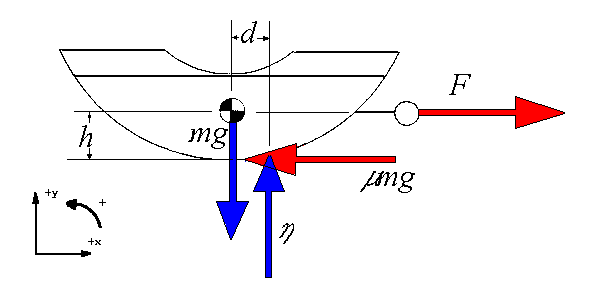
Figure 1

Equation 5 states the sum of the forces in the X direction is equal to the mass times the acceleration. If we pull the sled at constant speed using a horizontal force F, then the translational acceleration in the X direction (a_x) will be zero and hence the total force in the X direction will also be zero.

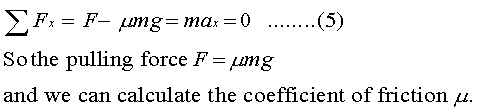
Similarly, equation 6 states the sum of the forces in the Y direction is also zero as the sled does not accelerate upward. The road exerts a contact force on the sled, represented by the Greek symbol eta (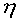) in Fig.1,.

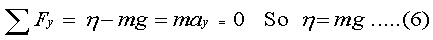
Next we examine whether the forces will produce a rotation. The rotational (angular) acceleration is proportional to the resultant torques. Torques are caused by the same forces but do not enter the calculation of translational acceleration. The magnitude of a torque is determined by the size of the force and the lever arm from the axis (usually taken as the center of mass) to the line along which the force acts. Notice the forces do not enter directly into the rotational motion - only their torques do. Forces and torques are never put into the same equation.

If we were not pulling on the sled then the only two forces would be the weight and the contact (normal) force of the road and they would have the same line of action i.e. the contact force would act along the vertical line through the center of mass (CM) just as the weight does. Both their torques about the CM would then be zero. "Normal force" means "force perpendicular to the road" and not "usual force".

When we pull through the center of mass as in Figure 1, the frictional force produced acts at road level and has a torque about the CM. The sled then tips up slightly so that the contact force no longer acts through the CM but moves forward. In the process it produces a torque which counteracts the torque due to the friction. The weight and pulling force do not have any torques about the CM as they pass through it.

Summing all the torques about the center of mass (though any other axis would do as well), we see that they must also sum to zero if the sled is not to accelerate rotationally.

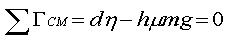
This balancing occurs automatically by the sled tipping up so that the normal (contact) force moves forward just sufficient to make its torque cancel that due to friction.

This is exactly our goal when pulling a drag sled. We try and have the forces in equilibrium so that you can equate the pulling force with the frictional force. This is why pulling horizontally and at a constant speed is important. If the speed is constant there is no acceleration. This results in the pulling force and the frictional force being equal though opposite and enables us to calculate the friction from the measured pulling force. At the same time we have the torques in equilibrium so that the sled is not rotating.

If we do not pull through the CM, then the pulling force will also have a torque about the CM. If F is acting above the CM, its torque will add to that of the friction and the sled will tip up further before coming into equilibrium. If F is acting below the CM then it will oppose the torque due to friction and the sled will not tip up as far before coming into equilibrium.

We can calculate the torques about any axis that is convenient. In Figure 1 above, the torques were summed about the center of mass. There is nothing important about this location. If the object is in rotational equilibrium about one axis, it will be in equilibrium for all axes. If you pull through the center of mass, then the pulling force has no torque about an axis through that point but the other forces will have torques about that axis, and those torques will need to be balanced if the sled is not to rotate.

Conclusion #1: Pulling through the Center of Mass is irrelevant to the measurement of friction using a drag sled.

2) How could the drag sled be built differently to minimize the shifting normal force?

Answer: Although the normal force moves forward to cancel the torque due to friction, this is not a desirable situation. The frictional force varies slightly with the nature of the surface. The normal force then moves its line of action back and forth to compensate. This means that the amount the sled tips up varies and leads to "chatter".

On the other hand, if we could pull at road level then the torques due to the pulling force and the frictional force would cancel as their lines of action would be exactly the same but they are in opposite directions. Since the torque due to friction has been canceled, the normal force will not move forward and it too will not produce a torque about the CM. The free body diagram of this situation is presented below in Figure 2.

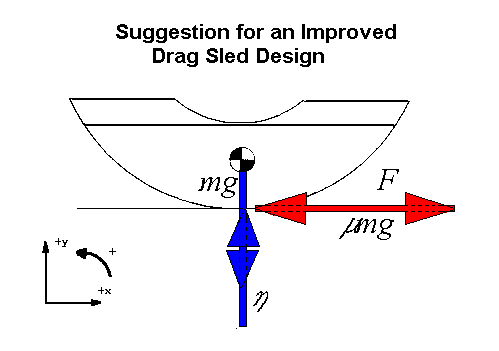
Figure 2

As h approaches 0, d also approaches 0 in Figure 1. The "chatter" is then greatly reduced.

Conclusion #2 It is clear the point of application for the pulling force can not be exactly at road level. If this were so the pull ring would drag the road. But, since most drag sleds are homebuilt devices, why not build them with the pull ring as low as possible. The closer to road level the pulling force the better. This will result in a much more stable drag sled.

3) Does the changing location of the normal force affect the drag factor calculated with equation (1)?

Answer: No. The changing normal force only contributes to drag sled instability.

He can be contacted at pheb@giraffe.ru.ac.za

Copyright ©