
The Traffic Accident Reconstruction Origin -Approach Angles Problem-


The Traffic Accident Reconstruction Origin -Approach Angles Problem-
|

|
You arrive at the scene of an urban traffic death to find the following:
Physical Evidence
Prominent skid marks lead back from a stopped vehicle. There is a noticeable gap in one set of skid marks. There is recent contact damage to the lower left front of the vehicle. A dead body is lying in the roadway. The victim is 6' tall.
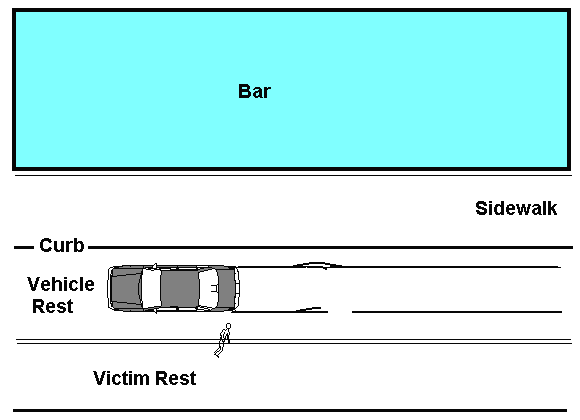
Figure 1
Two witnesses are available. They tell the following stories.
Witness 1: He states that he was standing outside the bar. Witness #2 and the victim began arguing. The victim was standing on the edge of the curb when Witness #2 pushed the victim toward the road. The victim lost his footing and fell into the path of the oncoming vehicle. The vehicle began to skid then ran over the victim.
Witness #2: He states that the victim was intoxicated, loud and unruly. The victim was standing on the edge of the curb. As he attempted to calm him, the victim's eyes rolled back into his head and he fell unconscious into the path of the oncoming car. The oncoming car skidded over the victim.
Physical Evidence
Examining the vehicle you can see that contact damage to the front of the car is all lower than bumper level. More specifically, the damage is to the lower part of the bumper cover on the driver's side. A careful examination of the victims clothing reveals a tire mark across the clothing that crosses at the victim's waist.
Examining the skid marks you observe a gap in the left side skid marks. Consistent with the gap in the left side skid marks is an irregularity in the right side marks.
You conclude from the damage to the vehicle that the pedestrian was lying down when he was struck by the car. Given the additional information of the tire mark on the clothing, the gap in the left side skid marks and the irregularity in the right side skid marks (indicating a vertical imbalance in the skidding vehicle) you know the location of the pedestrian when he was run over. This distance places his waist 10 feet from the curb edge.
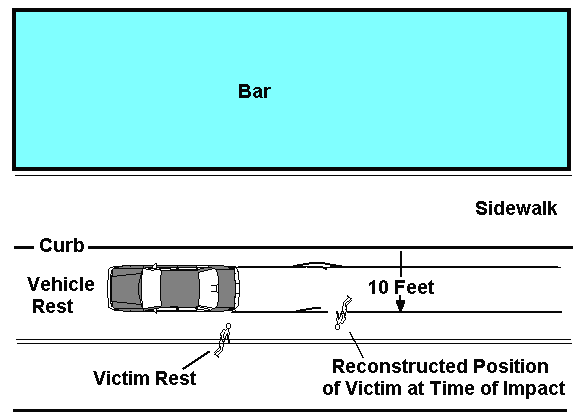
Figure 2
The falling victim can be modeled as a uniform long slender rod with length
l (r = l/2) and weight W,
traversing angle ![]() at angular velocity
at angular velocity
![]() as illustrated in Figure 3.
as illustrated in Figure 3.
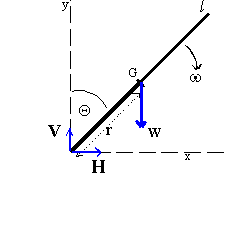
Figure 3
Question Posed: Which witness is telling a story that can be verified with the physical evidence and why?
|
Copyright ©
|