
The Traffic Accident Reconstruction Origin -Approach Angles Solution-


The Traffic Accident Reconstruction Origin -Approach Angles Solution-
|

|
by Dan Kemble
The collisions presented in the "Two Inline Collisions" case study are, although different in vehicle configuration at impact, very similar in nature with respects to vehicle speed analysis.
The first collision involves two vehicles. An eastbound, 4000 pound, red vehicle was stopped in the lane of traffic when it was struck in the rear by a second eastbound vehicle. The second vehicle was blue and weighed 3000 pounds. The driver of the blue vehicle applied the vehicle brakes at the moment of impact. After impact, both vehicles slid as a unit for 66 feet to rest on a roadway with a drag factor of .65. Each vehicle left four skid marks from impact to rest.
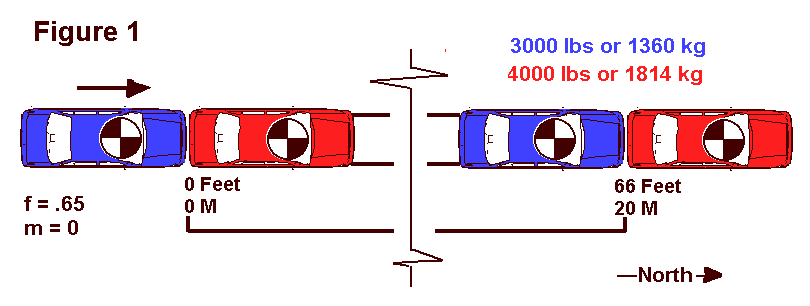
The second collision involved the same two vehicles (assuming some amazing government agency was able to rebuild them as "Bionic Vehicles" after the first heck-of-a-wreck!). This time, the 4000 pound red vehicle stalled out in the roadway facing northbound, giving the driver of the eastbound 3000 pound blue vehicle a beautiful target on the driver door. The vehicles collided and again slid to rest as a unit for 66 feet with all wheels locked.
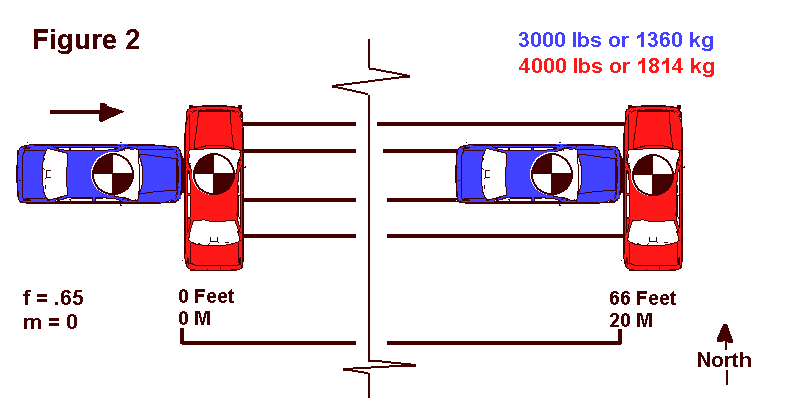
Both of the collisions as depicted in the diagrams are central impacts. That is, the principle direction of force was directed through both vehicles' center of mass. This results in no post-impact rotation in either vehicle.
Before answering the questions posed in the case, the post-impact velocity of the sliding vehicles must be calculated. In the first collision, both drivers were on the brakes. So, all eight wheels available to the post-collision unit were skidding. The eight wheels available post-collision in second collision are also "locked." In this case the brakes provide the lock-up for the blue vehicle. The tires of the red vehicle sliding laterally across the roadway provide the same resistance as if they were locked by braking. So all vehicles in both collisions have all tires locked after collision.
The post-impact velocity of the vehicles as a unit was:
![]()
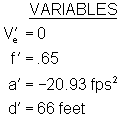
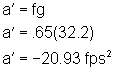

So, the post collision speed of the combined units in both collisions is 52. 56 ft/sec (35.85 M/h or 57.7 km/h).
Question 1
In collision 1, the pre-collision speed of the red vehicle was 0. What was the pre-collision speed of the blue vehicle?
Because the collision is in-line, where the center of masses of the vehicles are aligned to allow the transfer of momentum through the center of mass of the target vehicle, the in-line momentum equation can be used to establish the pre-impact speed of the bullet (blue) vehicle. The equation has already been modified to account for the vehicles post-impact movement as a unit.
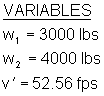
Calculations
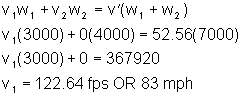
The pre-collision speed of the blue vehicle was 83 mph (133.6 km/h).
Question 2
In collision 2, the pre-collision speed of the red vehicle was 0. What was the pre-collision speed of the blue vehicle?
This collision is, as we have observed, the same as the first in that all forces applied to both vehicles are directed through the vehicles' center of mass. This is apparent with the additional given information that the red vehicle's initial speed was 0. The 90 degree, center of mass to center of mass collision configuration lends itself to a full impact in which the vehicles will attain a common velocity. Although the equation used above will work in this collision as well, I have applied the components to the 90 degree momentum equation for the target vehicle.

Calculations

The pre-collision speed of the blue vehicle was 83 mph (133.6 km/h). The two methods of calculating the speed for the target vehicle resulted in the same conclusion: the blue vehicle was traveling WTFF (Way Too Friggin' Fast)!!!
Question 3 & 4
3) What is the Delta-V (velocity change) for each vehicle in collision 1?4) What is the Delta-V (velocity change) for each vehicle in collision 2?
Because the variables for each collision are the same in respect to velocities (pre and post-impact) as well as the change in pre and post-impact angles (0), the calculations for each vehicle's Delta-V will be the same for both collisions.
Blue Vehicle
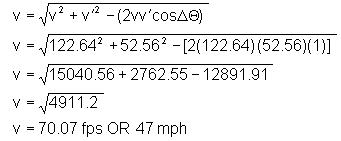
Red Vehicle

The Delta-V for the blue vehicle was 47 mph while the Delta-V for the red vehicle was 35 mph. Because the red vehicle was stopped at the time of impact, it only makes sense that the change in velocity it experienced was equal to the post-impact velocity of the two vehicles as a unit. Notice also that since this was an inline collision the Delta-Vs add back to the initial speed of the blue car. That is 47m/h + 35m/h = 83 m/h
Question 5
Is the Delta-V (velocity change) different for the red vehicle in collision 1 and collision 2?
The Delta-V experienced by the red vehicle in each collision was the same. The red vehicle is stationary when it is hit by the blue vehicle traveling at approximately 83 mph. The post collision speed is 35 m/h. The Delta-V of 35 M/h is identical.
Question 6
Would we expect the driver of the red vehicle's injuries to be better, the same, or worse in collision 2 when compared to collision 1?
I do not feel that the injuries would be as severe in collision 1 as they would be in collision 2. Here is why:
Although the Delta-V is the same, the time over which it was applied was greatly different. The driver of the red vehicle that was struck in the side will experience a greater acceleration than the driver who was rear ended.
Information on damage is not supplied. Nonetheless some generalizations can be made about injury. In collision 1 the red vehicle was rear ended at 83 mph. Its driver would no doubt sustain numerous injuries. I would expect to see major crush damage to the rear of the red vehicle as well as major crush damage to the front of the blue vehicle. A Delta-V of 35 mph, although very severe, could be survivable in this case due to the time over which the Delta-V applied to the driver. Delta-V over a specified time defines acceleration. This longer time would arise through the crushing of the vehicles.
Collision 2 involves a side impact collision, directly at the driver compartment of the red vehicle. Because of the relative weakness of vehicles to side impacts, the amount of crush to the blue vehicle would be lessened. This would cause more of the impact forces to be absorbed by the red vehicle and be seen as greater crush.
The proximity of the driver to the impact is also greatly reduced in this collision. In collision 1 the distance between collision and driver was at least 8 feet. In collision 2 the distance was closer to 8 inches. This difference in distances would decrease the time available to the blue driver to experience the Delta-V. This decreased time would raise the value of acceleration and likelihood for injury.
Finally, the speed of 83 mph would cause significant intrusion into the side of the blue car. Actual contact between the red vehicle and the blue vehicle's driver is possible, further decreasing the Delta-V time, increasing acceleration, and increasing likelihood for injury.
The prognosis for the driver of the red vehicle in the second collision is not good.
The two scenarios presented in this case would be very interesting to complete at scene investigations for. Collision dynamics, occupant kinematics and impact biomechanics all play an important role in understanding the entire reconstruction picture.
Dan Kemble is a nine year veteran of the Los Angeles Police Department, currently assigned to the Specialized Collision Investigation Detail. He has been investigating traffic collisions for the past eight years, and reconstructing collisions since 1995. Mr Kemble has completed approximately 440 hours of formal training in the collision investigation and reconstruction field. He is also a member of the Southwestern Association of Technical Accident Investigators (SATAI).
Mr Kemble operates "Southwest Collision Reconstruction."
He can be reached at kemble7@westworld.com
|
Copyright ©
|