The Traffic Accident Reconstruction Origin -Article-

Update on the Motorcyclist / Bicyclist Equation

Shortly after the paper "Estimating Vault Distance and Speed After a Motorcyclist or Bicyclist Ejection" was published, I was contacted by Jerry J. Eubanks of Texas A&M University’s "Pedestrian / Bicycle Accident Reconstruction School." Of primary concern to Mr. Eubanks was why pedestrian accidents were left out of possible uses of the equation. As a result, Mr. Eubanks and I applied this equation to some of his vast test data. The conclusion so far is: this is a valid equation and may be used to estimate vault distance and speed after a motorcyclist, bicyclist or pedestrian accident.

Second, the equation has undergone a "face-lift". It was rederived by Mr. Eubanks using units of feet and seconds rather than mixing feet with miles per hour. The resulting derivation is easier to understand as the trigonometric identities are not necessary. Also any rounding off evident in the original equations (30 in 30df) are eliminated, and the equation has been factored by another step. The ultimate difference is negligible, but it does make for a cleaner final product. I will present the new derivation and equation in this update. If you are already comfortable with the original equation you may still use it as before.

At the end of this update there is a short discussion on appropriate values to use for friction and angle in relation to pedestrian accidents.

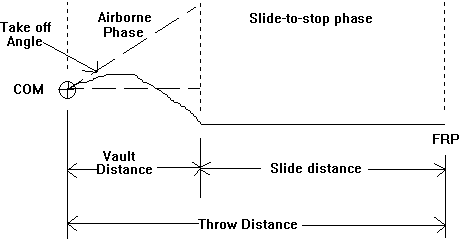
The graphical model of this derivation appears in figure 1.

The original equation used the speed (mph) equations for the slide-to-stop and airborne phases. The Eubanks derivation uses the velocity (fps) form of these two equations. Note: The original Eubanks derivation was performed in 11 steps. The author added some steps in this presentation to make it easier to understand.

One other difference should be mentioned. In the original equation the height the center of mass fell was entered into the equation as a positive number. This derivation requires that the height be entered as a negative number. This is because of the different airborne equation used in step 1 of this derivation:

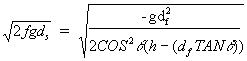(1)

Square both sides:

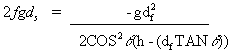(2)

Multiply the denominator to both sides:

(3)

Divide out -g to leave by itself and multiply the 2’s:

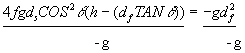(4)

Reduce:

(5)

Since we know the slide distance equals the throw distance minus the airborne distance , substitute this for the :

(6)

Divide both sides of the equation by (7)

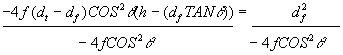(8)

Reduce:

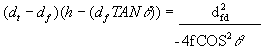(9)

Expand the left side of the equation:

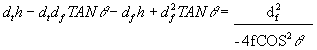(10)

Reduce

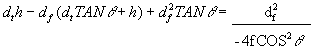(11)

Add 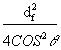to both sides:

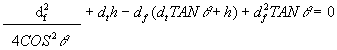(12)

Add the two terms which contain :

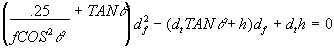(13)

This sets the values of the coefficients of the quadratic equation to:

(14)

The angle for a forward projection is 0° for all collisions of this type. The pedestrian drag factor you use should be the same as if a car with non ABS brakes slid on the same surface with all wheels locked. You may determine this in which ever manner you normally measure the coefficient of friction. This equation is extremely accurate when used this way.

For this type of trajectory the "normal" take off angles for pedestrians are 10 to 20 degrees. I have found the best place to start is by using a 10° take off. This angle should be combined with a friction value adjustment of 1.14 to 1.71. In other words, lets say you measured the friction at the scene and it was .80. Multiply .80 by 1.14 and then .80 by 1.71. In this case we get .91 and 1.3. Use these two numbers for the pedestrian’s friction value. This will get you in the "ball park".

Comparisons of this equation to test conditions were made against empirical testing performed by Jerry J. Eubanks and W.R. "Rusty" Haight. These comparisons show that this equation is very accurate for forward projections. Use of this equation for wraps is possible providing the reconstructionist follows the guidelines above. It is my opinion is that pedestrian equation models used in wraps are overly simplified. Only Jerry Eubank’s equation even considers the time the pedestrian is carried on the hood. Future work in this area should closely examine the exact trajectory of the pedestrian, then closer fitting models should be applied.

In addition to the acknowledgments given at the end of the first article, I would like to thank Jerry Eubanks for helping me realize this equation can be applied to pedestrian accidents. Jerry spent much of his own time on the phone with me, sending me crash test data, and sharing his opinions of the result of this equation when used with the test data. Thanks also to W.R. "Rusty" Haight and his side-kick, Buzz Light-year. Rusty teaches the Pedestrian / Bicycle course along with Jerry and was (and is) instrumental in the crash tests used to test this equation.

Palisades Interstate Parkway Police
P.O. Box 155
Alpine, NJ 07620
(201) 768-6001
or via Email: ASRich@Compuserve.com

Copyright ©