
The Traffic Accident Reconstruction Origin -Article-


The Traffic Accident Reconstruction Origin -Article-
|

|
An Introduction to Train Brakes
By John Bentley
Introduction
Imagine a vehicle that is a mile in length. It is so long that the front of the vehicle might be climbing a grade while the back is descending, or perhaps the front and back are turning left while the middle is turning right. This same vehicle is more than 300 times as long as it is wide. Next, imagine that it weighs more than 8 million pounds (3,700,000kg) or 4000 tons. Onboard the vehicle are televisions, foodstuffs and hazardous material. Now, visualize the vehicle is traveling at 70 MPH and the operator wants to stop.
This is a complex and challenging problem, but a situation that occurs thousands of times every day. The vehicle of course is a typical freight train. This short paper will introduce the reader to the principles of how train brakes accomplish this remarkable task.
Background
Freight train brake systems have not changed in basic operation since the 1930's. They are controlled and actuated by compressed air. For those tempted to think that train brakes operate the same way as large truck brakes read on. You might be surprised.
Each power unit (locomotive) has an air compressor that supplies air for the entire train's braking system. A feed valve in the locomotive regulates the desired pressure that is supplied to remainder the train. This pressure must be at least 70 psi (although most modern systems use 90 psi). A "brakepipe" runs the full length of the train. The brakepipe carries the compressed air from the control unit to the rest of the train. Unlike truck brakes (and passenger train brakes for that matter) this single source of air carries both the air that powers the brakes as well as the signal to control them.
|
Details of Brake Operation
Each rail car has its own brake system.
The brake components include a brake cylinder, brake shoes, a dual air
reservoir, and a control or AB valve. The AB valve is used to route air
from the reservoirs (auxiliary and emergency) to the brake cylinder. The
brake cylinders are connected through rods, levers and slack adjusters to
the brake shoes. While these components are similar to truck brakes their
operation is very different. Unlike truck brakes, train brakes are normally
off, or unapplied. The spring in the brake chamber is used as a return device
to pull the brake shoe away from the wheel and allow the wheel to roll freely.
So, in order to apply the brakes, air must be ported from the reservoir to the
brake chamber. There are several ways the engineer can apply
braking to the train. He selects the type of braking depending on the nature
of the stop desired. SERVICE BRAKES: This is the type of brake application normally used
for braking. This level of braking is achieved with a 6psi to a 26psi reduction
in the brake pipe pressure. When the AB valve senses the difference in pressure
air is ported from the reservoir to the brake chamber. Air pressure acts
against the diaphragm and brakes are applied. Braking with the Service Brakes
offers up to 75% of a train's Emergency Brake capability.
View a 80kb animation of Service Brake
Activation INDEPENDENT BRAKES: These are the brakes on the locomotive units only and do not apply brakes on any of the cars. While this brake method would effectively slow the locomotives if operated alone, this type of braking has only a minimal effect on a fully loaded train. These brakes are used in train handling, standing or any time a small brake level is needed on a train. They can give a braking level from none up to full independent, which is 75% of the locomotive's Emergency Brake capability. |
Flexible Hose Carries the Brakepipe between Cars
A Brake Chamber and associated Hardware

A Brake Shoe Removed from its Retaining Hardware and Held Against the Braking Surface of a Wheel |
POWER BRAKING: This means just what it says. When an engineer anticipates a problem may develop or desires to control the speed of the train, an application of the service brakes is made without reducing the throttle. When the train has slowed or the problem does not arise, then the train brakes are released and the train continues on, with the throttle still set. This type of braking has the advantage of reducing the time necessary to achieve Emergency Braking. This results in a quicker stop than an Emergency stop that was not preceded with Power Braking.
DYNAMIC BRAKES: Dynamic braking is using the traction motors of the units in a reverse flow so that they act to stop or slow the train. This type of braking is used primarily for train handling as it only slows the train via the locomotives. This type of braking cannot compare to train brakes.
EMERGENCY BRAKES: This is all the brake capability that a train has. It is utilized, as implied, when there is an emergency. Application of Emergency opens the brake pipe to atmosphere on all cars and units sequentially from front to rear. As a result, the AB Valves ports pressure from the Emergency reservoir to the brake chamber and all brakes slow the train. This type of brake use applies the brakes as fast as possible. An emergency application will cancel throttle to idle (see Power Braking above).
Special Considerations
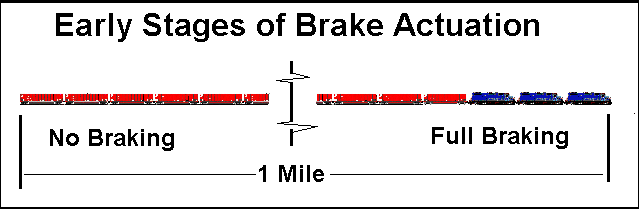
Utilizing air brakes on a vehicle that is more than 1 mile in length poses some interesting problems. Under ideal circumstances the air signal travels at about 920 fps. This occurs in Emergency, when the brakepipe is vented to the atmosphere. Thus, if a train was 5,526' long, it would take 6 seconds for the last car to sense the pressure drop and begin to start applying the brakes. The Federal Railroad Administration, under CFR Part 49, specifies the maximum time each car can take to achieve maximum braking. On trains operating at 70psi brakepipe pressure this maximum application time is 10 seconds. So, our hypothetical 5,526' freight train would take 16 seconds to attain full emergency braking. During this 16 seconds the train will have steadily increasing brake application taking effect between 1.5 (the time for braking in the first car to begin) to 16 seconds (the time the last car achieve full braking).
A second counter-intuitive situation exists with train brakes. Reconstructionists are accustomed to ignoring vehicle weight when calculating stopping distances. This assumption has validity for vehicles that skid to a stop. Trains on the other hand are designed with a maximum brake force that is below the force necessary to lock the wheels of an unloaded train. The effect of this is that maximum braking force is the same for loaded and unloaded trains and stopping distance is roughly proportional to weight. Stated another way, a train weighing twice as much will take about twice as long to stop. While this idea may be counter intuitive, it of course makes perfect sense for a vehicle with fixed maximum braking force.
Finally, train acceleration rates are severely restricted when viewed from a road vehicle's perspective. Cars and large trucks are capable of stopping at nominal rates of .75g. This stopping force originates at the tire-road contact area. It is limited by the friction coefficient between these two surfaces, rubber and asphalt, rubber and concrete, etc. All of these surfaces have dry surface friction coefficients near .75. Just like road vehicles, trains gather their slowing force from the wheel-track contact area. A typical friction coefficient for steel on steel is .25. This value is near the value of rubber on ice. So, it is not improper to view trains as perpetually driving on a surface that is equivalent to ice. The result is, when compared to road vehicles, trains change their speed very slowly. Despite the fact that a train reacts slowly, an engineer does have the ability to make meaningful changes in speed that could result in avoiding a collision. The following example will detail such an analysis.
A Typical Grade Crossing Analysis
An example of a time distance analysis follows. In this case a train was approaching a road crossing at 29 M/H. The sight distance available to the engineer was 484'. The question posed is how much could the engineer have delayed the train's arrival at the crossing by placing the train in emergency? That analysis follows.
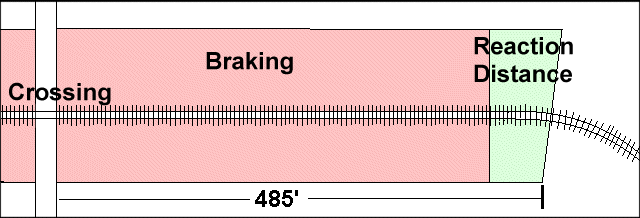
Total Available Distance = 485'
Initial speed = 29 M/H (42.5 ft/sec)
Estimated reaction time = 1.5 Seconds
TRAIN DATA
| Number of units (Locomotives) | = 2 |
| Length of units (Locomotives) | = 136.66 feet |
| Weight of units (Locomotives) | = 350.5 tons |
| Number of cars | = 18 |
| Length of cars | = 902 feet |
| Gross weight of cars | = 980 tons |
| Empty weight of cars | = 540 tons |
| Train length | = 1038 feet |
| Gross weight of train | = 1330 tons |
| Empty weight of train | = 890 tons |
| Brakepipe pressure | = 90 psi |
| Emergency propagation | = 1.128 sec. |
| Emergency braking efficiency | = 0.736 |
| Grade | = -.00173 |
First lets determine the Engineer's reaction distance using an average reaction time of 1.5 seconds.
Reaction distance = (Reaction Time) x (Speed)
Reaction distance = (1.5 seconds) x (42.5 ft/second) = 64 feet.
Subtracting this reaction distance from the total distance of 485' leaves 421' feet for the train to slow.
Next let's determine how long it would take the train to arrive at the crossing if the engineer did not act.
Distance/Rate = Time
(421 feet) / (42.5 ft/second) = 9.89 seconds
Next, we must calculate the actual slowing for the train. This is not a simple calculation. Recall we must account for the time for the air to propagate the length of the train. Next, the actuation time of the brakes for each car must be considered. We must also determine the weight of the train then compare it to brake force. The results of these calculations will be presented in the table below without support.
|
Initial Speed (mph) |
Stopping Distance (feet) |
Time to Stop (sec) |
|
29 |
712.1 |
25.89 |
The first thing that is apparent is that the available stopping distance of 421' is well less than the 712.1' feet required for the train to stop. The conclusion: The train can't stop before it gets to the crossing. But perhaps more interesting is the comparison of the time it takes the train to reach the crossing with and without braking. Again, this involves detailed calculations beyond the scope of this treatment. The result will be presented for purposes of comparison. Given the 421' brake distance the train arrives at the crossing at 24.14 M/H. The time it arrives is 10.46 seconds after the point the brakes were first applied. This time should be compared to the time required to reach the crossing if no action was taken. That time calculated above was 9.89 seconds. The difference is .57 seconds. This difference in time is not much, but perhaps sufficient for one additional car to make it across the crossing.
Conclusion
When compared to other modes of ground transportation trains have some unique characteristics that require special analytical consideration. The length of a train and its associated pneumatic brake systems, determining the train weight and calculating brake force are all variables that appear in stopping distance calculations. While running steel wheels on steel tracks greatly increases a train's load-carrying capability, these materials limit the ground forces available so that velocity changes in trains occur relatively slowly.
These problems notwithstanding, This truly massive vehicle travels thousands of miles daily with infrequent incident.
Mr. Bentley can be contacted at jb@train-dynamics.com
|
Copyright ©
|