The Traffic Accident Reconstruction Origin -Article-
|
The Traffic Accident Reconstruction Origin -Article-
|
|
Error Analysis for Skid Tests Method 3- Skid Tests Skid test convention recommends driving the vehicle at a known speed, locking the brakes, measuring the stop distance, then calculating the result. The results should be within 5% of each other. The following data was obtained in a skid test on a paved surface. Time: Surface: Asphalt Roadway, Time: 4:15 PM, Date 2/28/96, Vehicle 1994 Chevrolet Caprice (ABS defeated), Test Speed 40 M/H, Number of Samples: 2. Distance Data (Feet)
|
71 |
75 |
We will use the same equation to determine uncertainty:
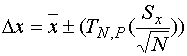Equation 1
Where,
= 73 - The average
(mean) of the tests
= 2.82 - The Standard
Deviation of the tests
= 2 - The Number of
tests in the sample
= 4.30 - The t
estimator from the table with 10 samples at 95% probability (note: this value does not
appear in the accompanying Student-t Table. Instead, it was taken from a more extensive
table published in another text).
= 13.1 Our answer
for uncertainty in Distance - The range in which the actual value of distance lies at 95%
probability.
Assuming the speedometer is calibrated, the uncertainty in speed is estimated at 1 M/H (certainly true with a digital speedometer)
Next, we must examine how these uncertainties propagate through the equation to drag factor.
The Equation for drag factor from a skid test is
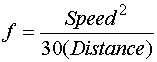
Uncertainty propagates to the drag factor through the partial derivatives of this equation. Those partial derivatives are
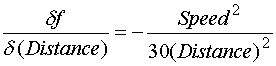
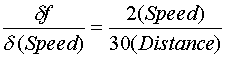
Using the average value for distance calculated as 13.1 feet, and the speed of the vehicle as 40 M/H. yields the following sensitivities.
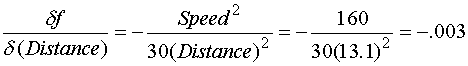
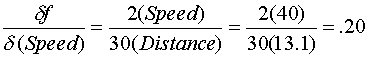
Using the uncertainty value for distance calculated above as 13.1, and an uncertainty of 1 for uncertainty in Speed yields the following for uncertainty propagated to the calculated drag factor.
Uncertainty in Distance propagated to drag factor is
Uncertainty in Speed propagated to drag factor is
And finally, the total uncertainty in drag factor is the sum of these two values or .2+.039=.24.
So, we can express the results that there is a 95% probability that the true of the drag factor is .73 +- .24.
|
Copyright ©
|