The Traffic Accident Reconstruction Origin -Article-
|
The Traffic Accident Reconstruction Origin -Article-
|
|
Special Student-t Table * It is recommended that the reader print this page to work the example problems.
|
Probability Percent |
t(50%) |
t(90%) |
t(95%) |
t(99%) |
|
|
Number of Tests n * |
|||||
|
5 |
0.741 |
2.13 |
2.77 |
4.61 |
|
|
10 |
0.703 |
1.83 |
2.26 |
3.25 |
|
|
15 |
0.692 |
1.76 |
2.15 |
2.98 |
|
|
20 |
0.688 |
1.73 |
2.10 |
2.86 |
|
|
30 |
0.683 |
1.70 |
2.04 |
2.75 |
|
|
40 |
0.681 |
1.68 |
2.02 |
2.70 |
|
|
50 |
0.680 |
1.68 |
2.01 |
2.68 |
|
|
Infinite |
0.674 |
1.65 |
1.96 |
2.57 |
This table is used to find the t-estimator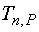 
.
For example the t-estimator for 5 tests (n=5) at 99% probability
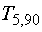is 2.13. Similarly
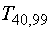=2.70.
Several observations can be made from simply examining the table.
Recall that the t-estimator is a factor for that is used to multiply Standard
deviation to determine uncertainty. It should then be apparent that choosing a smaller
probability will result in a smaller value for uncertainty. For example the t-estimator
for 20 samples at 50% probability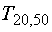 
is .688,
while the 99% t-estimator for 20 samples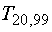 
is
2.86. Similarly, trials with more samples will also reduce the range of uncertainty.
This is illustrated by the observation that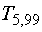 
is greater than 
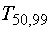(4.61>2.68).
The lesson offered by the table is that high probability estimates result from repetitive measurements.
*
This table may be used accurately with the equations supplied within this article. The reader may note that this abbreviated Student-t table has values slightly different that other such tables. This difference arises from the simplifying step listing Number of Tests rather than
(degrees of freedom) in the left column.
Other tables typically list
(= n-1) in the left column. Cell values in this
table have been adjusted to the index n rather than
.
|
Copyright ©
|