The Traffic Accident Reconstruction Origin -Article-
|
The Traffic Accident Reconstruction Origin -Article-
|
|
Drag sleds are widely used drag factor testing devices. The use of a drag sled to measure the drag factor of a particular road is simple process.
1) First the drag sled is weighed (W) with a spring scale.
2) The drag sled is then pulled across the surface in question via the spring scale. The force required to pull the sled (F) is measured on the scale as the sled is pulled at a constant speed.
Given these two values the drag factor is found with equation (1)
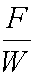
Though some drag sleds are manufactured and sold commercially most are home built devices. The typical example will be constructed from part of a tire filled with concrete. Several articles have been published on drag sled construction (1). Without fail all these articles point out the care that should be taken in the construction process to be sure that the pulling attachment point causes the force to act on a line through the center of mass.
A free body diagram is a way to examine forces that act on an object. What follows is a free body diagram of a drag sled sitting at rest on a horizontal surface.
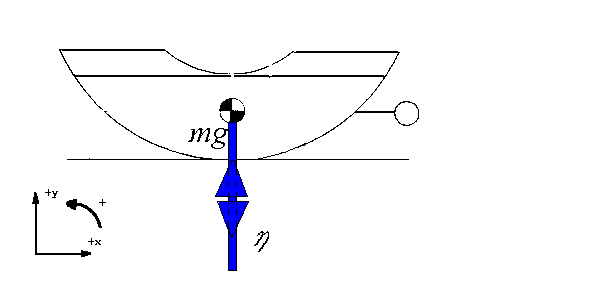
In the y direction,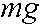 
opposes 
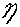. So,
(3)
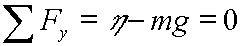
Here 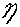represents the distributed contact force of the road surface against
the tire, or the normal force.
(4) 
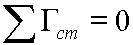
Next, the question arises what happens when we pull a drag sled at a constant speed
over a surface with a friction coefficient of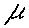 
. A free body diagram of that
situation follows.
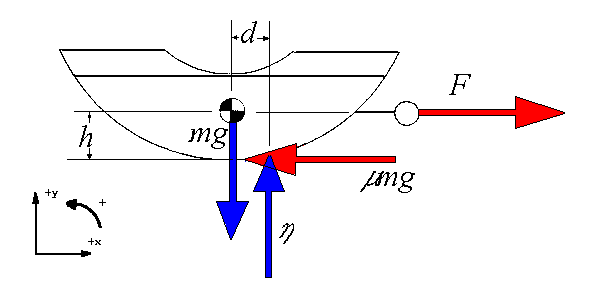
From this diagram we can see the sum of the forces in the x direction is 0:
(5)
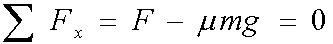
and the sum of the forces in the y direction is also 0,
(6)
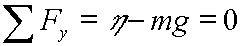
Summing the torques about the center of mass we see that:
(7)
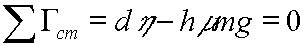
It is clear that the distance
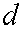will change as function of the frictional force
.
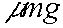(8)
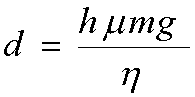
The questions posed are:
1) Why do we pull through the center of mass?
2) How could the drag sled be built differently to minimize the shifting normal force?
3) Does the changing location of the normal force affect the drag factor calculated with equation (1)?
|
Copyright ©
|