
The Traffic Accident Reconstruction Origin -Article-


The Traffic Accident Reconstruction Origin -Article-
|

|
Preface
The following articles describe an equation I derived following a fatal motorcycle ejection. The first
describes the theory and original derivation. The second article was written after communicating with
Jerry Eubanks of Texas A&M's Pedestrian / Bicycle Accident Reconstruction course.
I am very pleased with the accuracy of the equation when used in forward-projection pedestrian accidents. I believe, however, that equation models for wrap trajectories are over simplified; only Jerry Eubank's equation accounts for the time a pedestrian is "carried" on a vehicle. My equation is also over simplified for wraps: it just happens to give a reasonable estimate when the pedestrian's drag factor is adjusted. It is this adjustment which overcomes the oversimplification of the equation's model. Future work in this area should begin with redefining the base model of wrap trajectories: we should strive to make it more representative of the pedestrian's actual path. Contact (or no contact) with the windshield should be incorporated into this model. This should yield an equation which works on its own merits--without the help of adjustments.
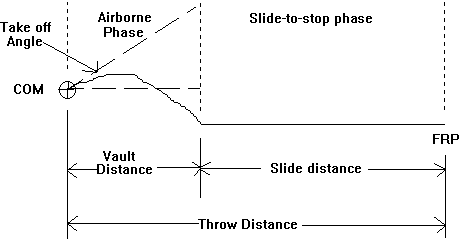
Estimating Vault Distance and Speed After a Motorcyclist or Bicyclist Ejection
By Sgt. Andrew S. Rich
Introduction
This paper describes a process in which the speed of a motorcycle or bicycle can be estimated at the time it ejects the operator. For the purposes of this paper, a cyclist’s ejection is considered to occur in two phases. Phase 1 is the distance that the cyclist is airborne and phase two is the distance from where he contacts the ground and slides / tumbles to his final resting point (FRP). The difficulty in estimating a speed due to ejection of a cyclist is determining the spot where the cyclist first contacted the ground after he was ejected. This spot is often impossible to locate. If this spot could be determined, the reconstructionist could then determine a vault distance and a slide-to-stop distance and use the appropriate equation to estimate a speed. What usually can be measured at the scene is the distance from the point of ejection to the FRP. This distance is known as the throw distance1. This subject has been examined before and equations do exist to estimate the cyclist speed knowing only the throw distance. Most notable is the Searle equation which yields a range of speeds. After some research however, the author was unable to locate previous work which considered the cyclist’s center of mass (COM) displacement in conjuction with the take-off angle. He also wanted to be able to use some type of calculations at the scene of an accident which would narrow the search for the first contact point. Previously, Collins used an iterative solution to calculate this distance after a pedestrian accident2. Collin’s approach however does not consider the angle of ejection.
Two issues need to be addressed before going any further. The first is the coefficient of rebound [restitution] (COR). An airborne object will obtain some component of vertical velocity which is independent of its horizontal velocity. Upon striking the ground the object will bounce (rebound). The vertical velocity change is directly proportional to the COR, i.e., higher CORs result in a greater vertical velocity change. Therefore the horizontal velocity is destroyed by friction more quickly.3 What this means to the reconstructionist is that not accounting for the COR may result in a lower speed estimate. The COR for most objects is unknown, although probably fairly small.4 This results in little horizontal velocity being destroyed. Another factor to consider is the method in which the drag factor for a tumbling body was empirically derived. It is doubtful that the published drag factors were corrected for the COR. This further reduces the need to consider it in this analysis.
The second issue that needs to be discussed is our friend the 45° angle
which is used by many reconstructionists to estimate a minimum speed when using the vault
formula. The author is aware that the correct method of determining the minimum speed
angle is by using the formula, ![]()
Since we do
not know the distance he was airborne, we cannot use this formula. Therefore a 45° angle
should be used with this process to calculate a minimum speed. Anyone who has used the
formula above and compared it with the results of the 45° angle can tell you that the
difference is negligible.
Measurements and Data
Measurements and data that need to be collected are as follows:
The Process
We must first calculate the horizontal distance the cyclist is in the air (vault distance). Without this process we could guess the distance. We then subtract the vault distance from the throw distance to determine the slide distance. We would then calculate a speed using the slide-to-stop formula and a speed using the vault formula. If the two speeds are equal then we estimated the correct vault distance. More than likely the speeds will not be equal, so we will have to try again and again until the speeds are equal. We could also program a computer to do the calculations over and over for us, or we can derive an equation that will calculate the vault distance without iteration. If we do this at the scene of the accident, we can then confine our search for the first contact point by measuring out the calculated vault distance.
The Equation
The complete derivation of this equation appears at the end of this paper.
The following variables are used in this equation:
q Take-off angle
h Vertical height center of mass was displaced. Positive if it landed lower, negative if higher.
![]() Throw distance
Throw distance
![]() Vault distance
Vault distance
![]() Slide distance
(=
Slide distance
(=![]() )
)
Since the vault speed should equal the slide to stop speed, we set these two equations equal to each other.
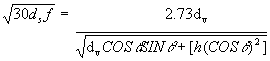
After several steps of derivation, we come to the following equation:
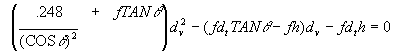
Looking closely at this equation we see that it is in the form of a general
quadratic equation, ![]() . In our equation,
. In our equation,
![]() becomes x of the quadratic. The following details the
rest of the coefficients:
becomes x of the quadratic. The following details the
rest of the coefficients:
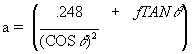
![]()
![]()
To solve for ![]() we use the quadratic
equation,
we use the quadratic
equation, 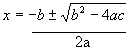
Remember that for our purposes ![]() becomes x. So the quadratic equation becomes
becomes x. So the quadratic equation becomes 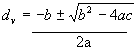
Recall that the solution of any quadratic equation yields two correct answers;
a positive and negative root. The positive root will be the answer that we need for this process.
The negative root would yield a negative vault distance which is obviously incorrect for this situation.
Now that we have the vault distance we can use it in the airborne vault equation to obtain the speed at
the time the motorcycle operator was ejected. To check our work we calculate the slide distance
(![]() =
=![]() ) and use this in
the slide-to-stop equation. Both speeds should be the same (or very close).
) and use this in
the slide-to-stop equation. Both speeds should be the same (or very close).
One further note on this equation. When a take-off angle of 45° is used, the a, b and c coefficients of the quadratic are simplified to:
![]()
![]()
![]()
Sensitivity to variables
The following tables are the results of computer simulations programmed by the author. The standard variable values used in the simulations are:
Three tables follow. Each table increments one of the variables. The variables that are not incremented retain their standard values.
Drag factor increment results:
|
Drag Factor |
Vault Distance (feet) |
Calculated Speed (MPH) |
|
.5 |
97.29 |
37.29 |
|
.6 |
105.75 |
38.94 |
|
.7 |
112.8 |
40.26 |
|
.8 |
118.76 |
41.34 |
|
.9 |
123.86 |
42.25 |
|
1.00 |
128.29 |
43.02 |
Height increment results:
|
Height (feet) |
Vault Distance (feet) |
Calculated Speed (MPH) |
|
4 |
118.76 |
41.34 |
|
10 |
120.81 |
40.74 |
|
20 |
123.87 |
39.83 |
|
30 |
126.56 |
39.01 |
|
40 |
128.96 |
38.27 |
|
50 |
131.13 |
37.58 |
Angle increment results
|
Angle (degrees) |
Vault Distance (feet) |
Calculated Speed (MPH) |
|
5 |
62.17 |
55.38 |
|
15 |
91.97 |
48.50 |
|
25 |
108.60 |
44.19 |
|
35 |
116.66 |
41.95 |
|
45 |
118.76 |
41.35 |
Examination of these tables show that this process is most sensitive to the take-off angle. Unless a lower angle can be justified, a 45° angle will provide a conservative speed estimate. Varying the drag factor manifests less sensitivity to this variable. When using this process, it is recommended that the reconstructionist use high and low values for the drag factor. This process is least sensitive to the COM displacement (height). This works out well for us since it can often be most difficult to obtain if the roadway is not level. It would take a large margin of error to throw this equation off. Since this measurement feeds the airborne phase of the equation, it is always better to over estimate the height which will provide a lower speed estimate.
Case Study
The following accident was the impetus for developing this process. It occurred on a four lane highway with two lanes both north and south, separated by a grass median. The posted speed limit is 50 MPH. The road surface is asphalt which was dry at the time of the accident. This accident occurred in the south bound left shoulder which is 3 feet in width. The COF for the shoulder was measured with a drag sled and determined to be .65. The vehicle, a 1992 Honda Goldwing (Aspencade) is equipped with an integrated braking system. This system will activate the left front caliper by applying the rear brake. Inspection of the accident vehicle determined that this system was functioning properly. Tests done at Northwestern University Traffic Institute show that while the rear brake is easy to lock, the front brake will never lock when the foot brake is used alone. The drag factors achieved with this type of braking were always higher than those for a large car with all four wheels locked.7 For some unknown reason the motorcycle was on the left shoulder when the operator locked the rear brake. The motorcycle slid leaving a serpentine friction mark 156.9 feet in length. After sliding this distance the operator released the rear brake which was manifested by the sudden appearance of oblique striation marks in the rear friction mark and the beginning of a front tire scuff mark which also exhibited oblique striations. Both the front and the rear tire marks come to a sudden end soon after appearance of the striations. Nine feet after the end of the rear tiremark, a deep scratch about 3 feet in length is observed in the asphalt where the right side of the cycle contacted the ground. The motorcycle then traveled 161 feet to final rest on the grass median. Because instead of sliding, the motorcycle was severely tumbling and airborne for much of this distance, a slide-to-stop equation could not be performed. Too much energy was lost due to damaging the motorcycle and making large depressions in the ground to be accurate. Witnesses state that the cyclist was airborne after ejection from the vehicle. For a conservative estimate, the start of the long scratch in the shoulder was used as the point of ejection. From this point to the operator’s FRP was measured as 190 feet. The height of the cyclist’s COM was determined by using an exemplar motorcycle and a colleague who is about the same height as the victim. The COM was measured as 3.3 feet. A drag factor of .80 will be used for the cyclist who was tumbling rather than sliding on the median. Our facts for this equation are established and for a minimum estimate we will assume a take off angle of 45°
![]() = 190 feet
= 190 feet
f (body tumbling) = .80
q = 45°
h = 3.3 feet
Solve for a 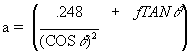 =
= 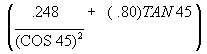
a=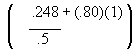 = .496+.80 = 1.296
= .496+.80 = 1.296
Solve for b b= ![]() =
= ![]() = -(152-2.64) = -149.36
= -(152-2.64) = -149.36
Solve for c ![]() = -[(.80)(190)(3.3)] = -501.6
= -[(.80)(190)(3.3)] = -501.6
Solve for ![]()
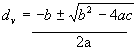 =
= 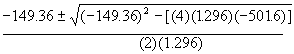
![]() =
= ![]()
![]() And
And ![]()
![]() 118.6 feet And
118.6 feet And ![]() -3.26 feet
-3.26 feet
As far as the quadratic equation is concerned, both answers are correct. However as reconstructionists we are only concerned with the positive root (118.6). We now take the vault distance and apply it to the vault equation. Because our take-off angle is 45°, the vault equation becomes:
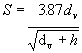 =
= ![]()
![]() =
= ![]() = 41.57 MPH
= 41.57 MPH
Check this using the slide-to-stop equation. Recall that
![]() therefore:
therefore: ![]() = 71.4 feet.
= 71.4 feet.
![]()
We can see that the two speeds concur with each other so we know our arithmetic is correct. Whenever possible, independent speed estimates should be used. Using Searle’s equation with this same data yields a minimum speed of 52.69 MPH. This is quite a difference. However, when the take off angle is reduced to a more reasonable 10°, the Searle minimum equation yields 52.69 MPH and this equation 51.87 MPH.
Now we calculate the speed loss from the rear tire skidmark.
F=.65
d=156.9 feet
![]()
Now combine the two speeds.
![]()
The motorcycle was traveling at a minimum speed of 69.1 MPH at the start of the rear tire skid mark.
If we use the 10° vault estimate of 51.87 MPH and combine it with the rear tire marks we get a combined speed of 74.37 MPH. With these two estimates we can say the motorcycle was traveling between 69 and 74 MPH at the at the start of the skid.
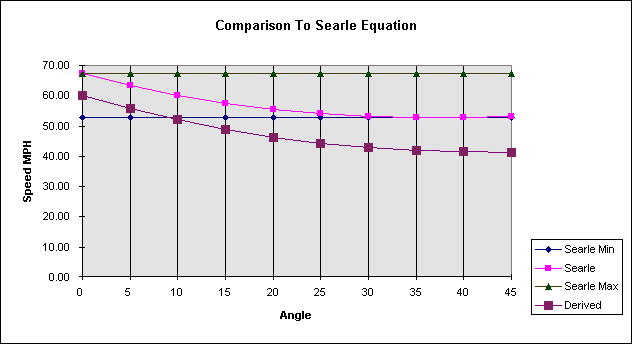
The graph shown above was produced with data from our case study. Examining the graph shows that this process produces the same curve as the basic Searle equation. What is interesting is the intersection of the Searle minimum plot with the derived value at about 9° which is a realistic takeoff angle. Can this intersection be the true speed at ejection? Comparing this process to the Searle minimum equation reveals that they are very close at normal take off angles. Direct comparison with Searle’s equation may not be appropriate in this case since Searle tested his equation against pedestrian throw trajectories. Pedestrian trajectories differ from ejection trajectories because they occur in three phases. That is, in most cases the pedestrian is carried on the car for some distance before the airborne phase begins. In most cases, the airborne phase for pedestrian accidents is a fall rather that a vault. All this aside, the best way of substantiating this process would be by empirical testing.
Conclusion
This process gives the reconstructionist another tool to estimate the speed of a motorcycle or bicycle at the time it ejects the operator. Although independent slide-to-stop and vault analysis can be used, many times finding the spot the operator first contacted the ground is not possible. By using this equation at the scene of an accident, the investigator can narrow the area of search for the first contact point. Slide-to-stop can also be applied to the distance the cycle slid on its side. If during the slide however, the cycle strikes one or more substantial objects or loses energy due to damaging of the vehicle or the surface it tumbles on, the estimate becomes too unreliable. This process may also be used in the analysis of a bicyclist ejection provided all the data required can be collected at the scene. In any investigation, the reconstructionist should employ all methods of analysis at his disposal. Using two or more independent means of analysis aids the reconstructionist in substantiating his conclusions.
Acknowledgments
The author gives thanks to Sgt. Joe Cofone, Inv. Jeff Weinberg and Inv. Greg Donatello of the Bergen County Prosecutor’s Office, Fatal Accident Investigation Unit for their thoughts and use of resources when researching this paper.
Derivation
The speed at the start of the airborne phase should equal the speed at the start of the slide-to-stop phase.
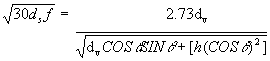
Square both sides.
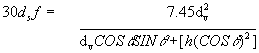
Cross Multiply and divide by 30
![]()
Perform the division.
![]()
Substitute ![]() for
for ![]()
![]()
Expand ![]()
![]()
Multiply two right terms
![]()
Divide by ![]() .
.
![]()
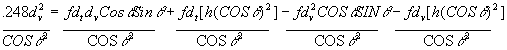
Perform the division. Recall that SIN/COS = TAN
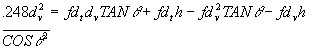
Add ![]() to both sides.
to both sides.
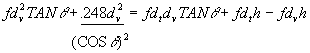
Complete the addition for the left side of the equation.
![]()
Simplify right side.
![]()
![]()
Set the equation equal to zero.
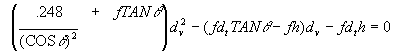
The quadratic equation is now used to solve for ![]() .
.
If q = 45° then
![]()
References
1
Eubanks, Jerry J and Haight, W.R., Pedestrian Involved Traffic Collision Reconstruction Methodology, Society of Automotive Engineers (SAE) SAE Technical paper# 921591
2
Fricke, Lynn B., Vehicle-Pedestrian Accident Reconstruction, Northwestern University Traffic Institute Topic #877 and Traffic Accident Reconstruction., 1990
3
Searle, John A and Angela, The Trajectories of Pedestrians, Motorcycles, Motorcyclists, etc., Following a Road Accident, SAE Technical paper #831622
4
Searle, John A and Angela, The Trajectories of Pedestrians, Motorcycles, Motorcyclists, etc., Following a Road Accident, SAE Technical paper #831622
5
Baker, J. Stannard and Fricke, Lynn B., Speed Estimates For Vehicles That Fall, Flip Or Vault, Northwestern University Traffic Institute Topic # 866 and Traffic Accident Reconstruction., 1990
6
Daily, J., Fundamentals of Traffic Accident Reconstruction, Institute of Police Technology and Management, 1988
7
Fricke, Lynn B and Riley, Warner W., Reconstruction of Motorcycle Traffic Accidents, Northwestern University Traffic Institute Topic # 874 and Traffic Accident Reconstruction., 1990
Palisades Interstate Parkway Police
P.O. Box 155
Alpine, NJ 07620
(201) 768-6001
or via Email: ASRich@Compuserve.com
|
Copyright ©
|