
The Traffic Accident Reconstruction Origin -Article-


The Traffic Accident Reconstruction Origin -Article-
|

|
Error Analysis for Three Different Methods Of Determining Drag Factor By Oren Masory and Bill Wright Introduction What is the best way to test for drag factor? This article will compare three different
methods from an error analysis perspective. The concepts introduced in two previous TARO
Articles,
Statistics - a Method to Quantify Uncertainty and
Sensitivity to Uncertainty will
guide these comparisons. Review- Error is found from Uncertainty and Sensitivity Regardless of how careful we are, or how much money we spend on the tool, no
measurement will ever be exact. This inexactness is called uncertainty. All measurement
contains uncertainty. It is a fact. It is always true. Given this limitation the prudent
measurer should have an understanding of the level of uncertainty that accompanies every
measurement that is made. For example instead of saying, "The skid mark is 62.5 feet in
length", the prudent measurer might say something like, "It is 62.5 feet plus or minus
.25 feet." Many measurements we make in the field of reconstruction are direct measurements.
Examples of direct measurements are: 1) The length of a skid mark measured by a steel tape. 2) The acceleration of a vehicle measured by an accelerometer 3) An angle measured by a transit On the other hand, some measurements are not measurements at all. They are calculated
values. Examples of calculated values are: 1) The length of a skid mark calculated with a total station. 2) A drag factor calculated with a drag sled or skid test 3) An angle calculated by the use of trigonometry with the measured sides of a triangle. The crucial distinction is that direct measurements are exactly that: determined directly,
calculated values result from a direct measurement applied through a relationship, usually
an equation. Quantifying error in a direct measurement can be determined from the uncertainty in
measurement alone. On the other hand, the act of calculating a value can also have an
effect on error. This effect is sensitivity to the calculation. In the following examples,
the effect of uncertainty and sensitivity will be used to quantify error in three different
methods for determining drag factor. Method 1 - An Accelerometer The following skid test was conducted in an accelerometer instrumented test vehicle.
This accelerometer is equivalent to commercially marketed skid test accelerometers like a
Vericom or g-Analyst. Surface: Asphalt Roadway, Time: 11:05 AM, Date: 05/12/98, Accelerometer:
CJ Enterprises Model CJA-6110 (Bandwidth 170Hz) Sampling Rate: 50 samples per second,
Skid Duration 2.2 Seconds, Number of samples: 110, Filtering: 10 point moving average,
Curve Fit: Linear- voltage to g. g Data
We will use the following Equation to determine uncertainty:
0.658, 0.655, 0.656, 0.647, 0.612, 0.602, 0.623, 0.636, 0.615, 0.615, 0.604, 0.624, 0.64
0.659, 0.690, 0.720, 0.771, 0.778, 0.785, 0.767, 0.763, 0.749, 0.741, 0.725, 0.702, 0.705
0.680, 0.685, 0.679, 0.686, 0.689, 0.701, 0.735, 0.739, 0.734, 0.751, 0.772, 0.760, 0.724
0.704, 0.699, 0.696, 0.692, 0.689, 0.715, 0.725, 0.732, 0.735, 0.732, 0.743, 0.747, 0.773,
0.783, 0.776, 0.786, 0.800, 0.797, 0.775, 0.766, 0.758, 0.750, 0.735, 0.728, 0.722, 0.711,
0.712, 0.694, 0.685, 0.680, 0.680, 0.696, 0.703, 0.725, 0.732, 0.739, 0.756, 0.778, 0.783,
0.792, 0.802, 0.813, 0.807, 0.794, 0.791, 0.789, 0.788, 0.787, 0.796, 0.792, 0.803, 0.792,
0.788, 0.786, 0.776, 0.771, 0.754, 0.754, 0.746
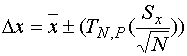 Equation 1
Equation 1
Where,
![]() = .742 - The average
(mean) of the tests
= .742 - The average
(mean) of the tests
![]() = 0.068 - The Standard
Deviation of the tests
= 0.068 - The Standard
Deviation of the tests
![]() = 110 - The Number of
tests in the sample
= 110 - The Number of
tests in the sample
![]() = 1.99 - The t
estimator interpolated from the
Student-t table with 110 samples at 95% probability
= 1.99 - The t
estimator interpolated from the
Student-t table with 110 samples at 95% probability
![]() = .013 Our answer
for uncertainty- This is the range in which the actual value of x lies at 95% probability.
= .013 Our answer
for uncertainty- This is the range in which the actual value of x lies at 95% probability.
Now we must examine the equation's sensitivity to error. The equation is:
![]()
This equation is trivial and states that the drag factor (on a level surface) is equal to the acceleration in units of g. Notice too that the partial derivative is also very simple. It states:
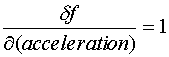
This result should not come as a surprise. In fact, the partial derivative of all direct measurements with respect to that measure is equal to 1. This is another way of saying that error is not compounded by sensitivity to calculations. There are no calculations with direct measurements.
What this error analysis means is that there is a 95% probability that the true value for drag factor lies between .742 +- .013.
So, in the case of the accelerometer, the entire error analysis procedure is accomplished by calculating uncertainty. The next case will not be so simple.
Method 2- A Drag Sled
Drag sled convention recommends multiple pulls across the surface in question. Once ten readings are taken. Those results are averaged to find the value of drag factor. The following data was obtained in a drag sled test on a paved surface.
Time: 9:50 AM, Date 6/6/86, sled weight: 54 pound sled, Scale: Hanson Model 8920, Number of Samples: 10 (Drag sled test conducted by J.F. (Jim) Mitchell jfmitch@bconnex.net)
Pull Data (pounds)
|
42 |
40 |
40 |
38 |
38 |
40 |
42 |
38 |
40 |
41 |
The entire calculations are available on a separate page.
Uncertainty in puling force is found with Equation 1.
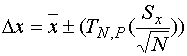 Equation 1
Equation 1
The resulting answer ,![]() , 39.9 +- 1.08 lbs.
This is our answer for uncertainty in pounds of pull, the range in which the actual value of
pull (x) lies at 95% probability.
, 39.9 +- 1.08 lbs.
This is our answer for uncertainty in pounds of pull, the range in which the actual value of
pull (x) lies at 95% probability.
We must also find the uncertainty in the value of weight of the drag sled. We will assume the scale to be calibrated. We will also assume that we are able to read to half the values incremented on the scale's index. The scale is indexed every 2 pounds, so the resulting uncertainty is 1 pound.
Next, we must examine how these uncertainties propagate through the equation to drag factor.
The Equation for drag factor from a drag sled is
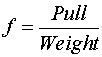
Uncertainty propagates to the measured value through the partial derivatives of this equation. Those partial derivatives are
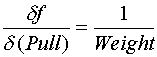
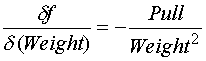
Using the Average value for Pull calculated above as 39.9 lbs. and Weight of the sled as 54 lbs. yields the following sensitivity.
The results of this drag sled test state that is there is a 95% probability that the true drag factor lies between .74 +- .033.
Method 3- Skid Tests
Skid test convention recommends driving the vehicle at a known speed, locking the brakes, measuring the stop distance, then calculating the result. The results should be within 5% of each other. The following data was obtained in a skid test on a paved surface.
Time: Surface: Asphalt Roadway, Time: 4:15 PM, Date 2/28/96, Vehicle 1994 Chevrolet Caprice (ABS defeated), Test Speed 40 M/H, Number of Samples: 2.
Distance Data (Feet)
|
71 |
75 |
As always, we will use the same equation to determine uncertainty:
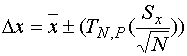 Equation 1
Equation 1
The details are
available elsewhere and calculate to a
![]() = 73 +-13.1 feet. This is our answer for
uncertainty in Distance - The range in which the actual value of distance lies at a 95%
probability.
= 73 +-13.1 feet. This is our answer for
uncertainty in Distance - The range in which the actual value of distance lies at a 95%
probability.
Assuming the speedometer is calibrated, the uncertainty in speed is estimated at 1 M/H (minimally true with a digital speedometer that only resolves in 1 M/H increments). Next, we must examine how these uncertainties propagate through the equation to drag factor.
The Equation for drag factor from skid tests is
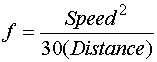
Uncertainty propagates to the drag factor through the partial derivatives of this equation. Those partial derivatives are
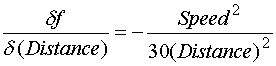
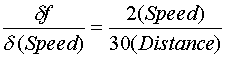
The total uncertainty in drag factor to a 95% probability from these skid tests is .73 +- .24.
Comparison of Results
The results for the error analysis of these three tests are presented in Figure 1 below.
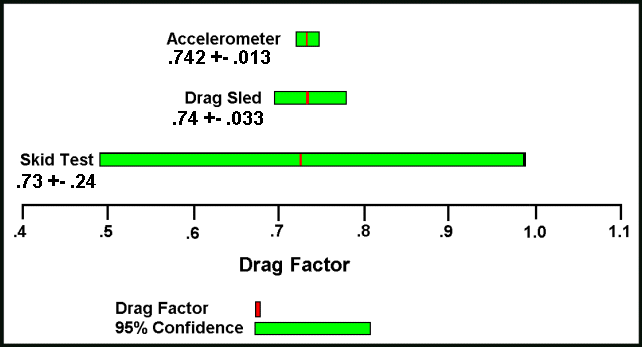
Figure 1
Graphed this way, the results are dramatic. Skid tests render values that are little better than guessing. In fact guessing might be better. Drag Sled values are about four times as good as the range offered in a drag factor table. Finally, the accelerometer tests are about three times better than the drag sled tests. (Note: These tests were assembled at random - your actual confidence levels will vary as a result of experimental technique, measuring equipment, and number of tests).
The reader should be curious as to why there is so much difference in the confidence intervals. A histogram of the results of these tests will help make the reason clear.
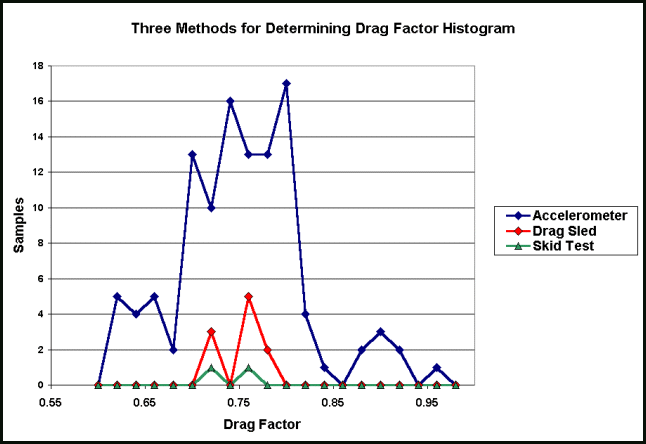
Figure 2
Figure 2 shows that the test with the accelerometer has the widest range of values and the Skid Test tests have the smallest range. It should also be clear that the accelerometer tests have the most samples and the Skid Test tests have the smallest. Given the previous calculations, the significance of repeated testing should be obvious.
It is also worthy of note that two accelerometer tests that collect hundreds of data points, but report only one point per test have all the same error considerations as the test skids in this analysis - very few samples.
Conclusion
High confidence estimates result from carefully conducted tests with large sample sizes applied to direct measurements. Low confidence levels result from poor technique, small sample sizes or calculations involving great sensitivity.
It is important to note that the results presented in this article evaluated three specific tests. This does not necessarily mean that one test method is better or worse than another, but it does offer some guidance on skid testing procedure. All the tools necessary to perform an error analysis are included in this article and relatively simple to apply. The prudent measurer should use them with each of his tests.
The moral to the story is clear: be careful in your technique and sample sample sample.
Dr. Oren Masory is a Professor and the Director Robotics Center of the Mechanical Engineering Department at Florida Atlantic University in Boca Raton, FL. He can be reached at (561) 297-2693 or via Email at masoryo@pop.fau.edu
Bill Wright is an accident investigator with the Palm Beach County Sheriffs Office in West Palm Beach, Fl (USA). He teaches accident investigation and driver t raining topics. He can be reached at bwright@tarorigin.com
|
Copyright ©
|